25 Feb Spins, shapes and much more
The strange world of quantum mechanics is very complex and hence difficult to understand. The best way to understand this weird world is to visualize it. Visualization is the formation of an image of our mind’s own imagination. And human brain is very well adapted to visualization. There are many concepts in quantum mechanics which are well understood by visualization such as wave particle duality, Schrödinger’s cat, superposition principle, Heisenberg’s uncertainty principle and many more.
My work is mostly concerned about the spins which is an intrinsic form of angular momentum carried by the elementary particles (such as electrons) and the composite particles (such as protons, neutrons). The dynamics of the spin system is governed by quantum mechanics which is described by some mathematical equations. Spin can be considered as a vector quantity which has a direction and a magnitude. The simplest
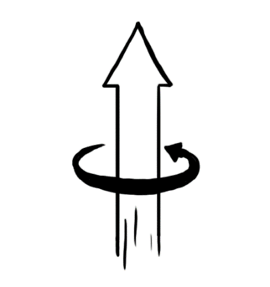
way to visualize a spin is to visualize it as an arrow which is precessing with definite frequency along the direction of magnetic field (Figure 1). That’s quite easy!!
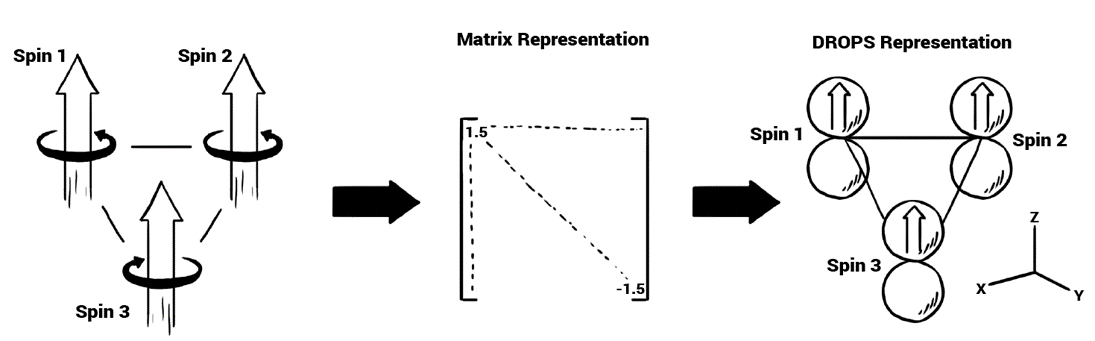
But imagine we are working with multiple spins and all of them have different precession frequency and all of them are connected to each other by an imaginary thread (in technical language this is known as coupling between the spins). In this case, the mathematical equations get messy and one may not be able to visualize their dynamics intuitively. How can we simplify this problem? It turns out that we can still visualize the spin system if the state of the spins is described as a matrix which can be then mapped to the set of spherical harmonics (these are some special functions defined on the surface of the sphere) which combine to form a shape of droplet as shown in this work. In simpler terms, a spin’s state and the advance concepts, which explain its dynamics such as product operator, density matrix, propagators, Hamiltonian etc., can be written
down in terms of matrix and these matrices can then be visualized as a set of droplets (figure 2)
As now we can visualize the spin in an intuitive way and one can also interactively explore spin dynamics by using the SpinDrops app. The next question that arises is ‘are these shapes real’ or ‘is it just an abstract imagination’? It turns out that all these shapes are real and in fact one can obtain these shapes experimentally as well. Some recent studies (here and here) underline the protocols for obtaining these shapes experimentally and this forms the theme of my current research work. This current work is focused on developing a protocol for the experimental reconstruction of the shapes corresponding to propagators which is commonly known as quantum process tomography in quantum computation
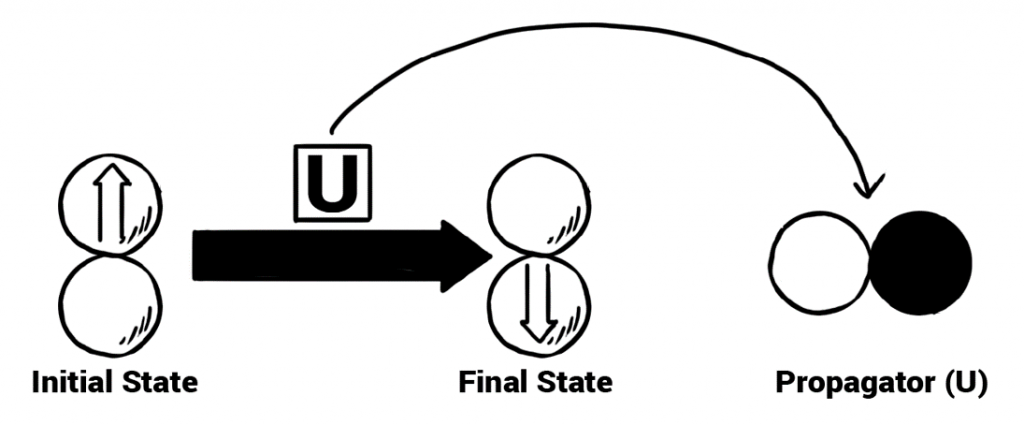
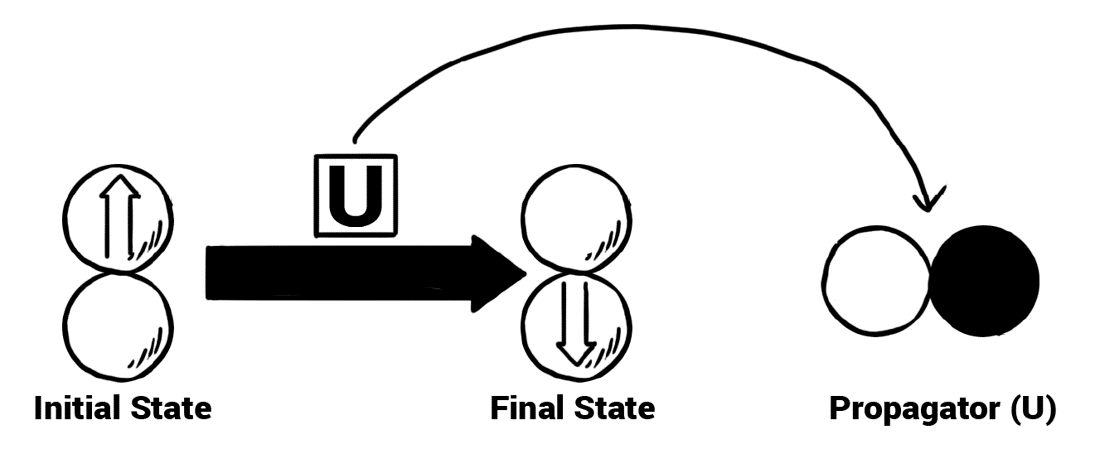
Before proceeding further, let us first understand what a process and a propagator is. A process consists of a set of propagators which drives the system from an initial state to a final state. And with the help of the approach discussed above one can visualize these propagators as a set of droplets (Figure 3) and by performing the desired experiments one can obtain these shapes experimentally. The work has already been done if the process is known and my current task is to develop the protocol to obtain the DROPS shapes experimentally for the unknown processes.
As evident from the current quantum computing and quantum information architectures (such as NMR, NV centers etc.) that spin is a promising candidate for a qubit and this kind of visualization method will surely help us to understand the dynamics of a complex system in a very simple way. More interestingly, these shapes are not merely an imagination they are a visualization of some mathematical equations and one can even obtain these shapes experimentally.


