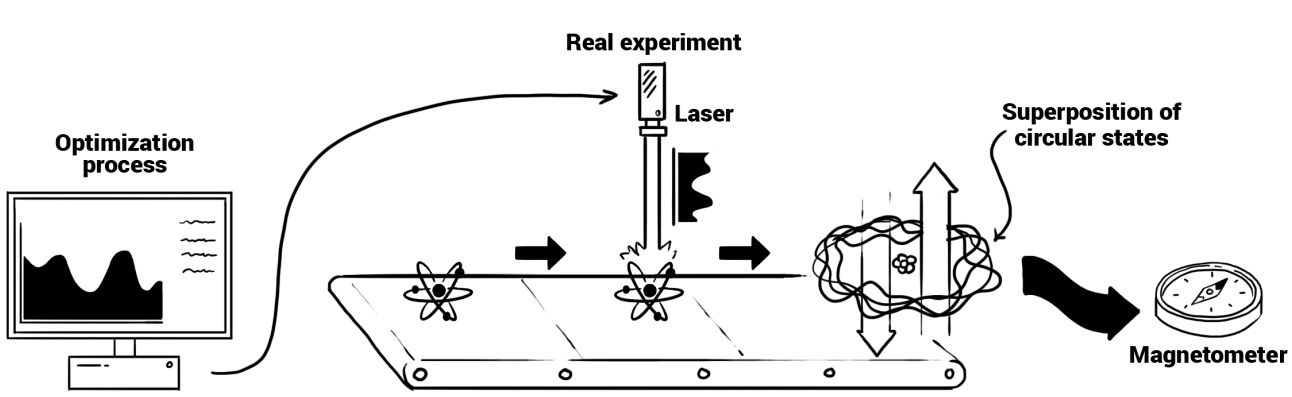
02 Sep Superposition of circular states in a Rydberg atom (or how to build a quantum compass)
A little bit of science and what we are looking for:
Rydberg atoms have become really useful in many different quantum technologies and processes. Basically, they are atoms with one highly excited electron, which is in an orbital far, far away from the nucleus. If the element used for the Rydberg atom is an alkali (any element in the first column of the periodic table) then we can simplify the model by approximating it to a hydrogen atom (with only one electron that has to be taken into account) with some minor corrections. And this is truly useful, because not only is hydrogen the simplest atom we can find, but also we, physicists, know that theoretical model like the back of our hand. After that approximation, we can characterise the state of the atom just by looking at the state of that single electron.
So far so good, right? Now, given an energy level there are two very important states in a Rydberg atom: the circular states. These states receive their name from the shape of their orbital, which looks like a donut, a shape which we call a “torus”. They are great because they do not suffer as much from the small fluctuations in our machines’ electrical field and they are very well protected from decoherence (the natural process in which the good quantum properties of our system would be lost).
It is about time to recall the very famous thought experiment from Schrödinger: a cat that can be dead and alive at the same time, that is, a superposition of both. This just illustrates the fact that one particle can be in a superposition of two different states in a quantum system. And that is exactly our objective: preparing a Rydberg atom in a superposition of two different circular states.
But why do we want this?
Simply because these atoms would be a great tool in metrology, the science of measuring physical quantities. More specifically, we are interested in magnetic fields. These are used in many different applications from brain resonances to archaeology.
And as one could imagine, the more measurements of a single quantity that we perform, the least error we obtain in the end. But here is the catch: classical systems and quantum systems are subject to different laws, and the accuracy that we can achieve in metrology is quite different. With a quantum (perfect) magnetometer, we would have to do 1,000 measurements to reduce our error to a factor of 0.001. With a classical system we would need at least 1,000,000 measurements to achieve the same result! That is why quantum technologies are so important in metrology.
How do we do it?
In the physical experiment, a beam of rubidium Rydberg atoms (which happen to be an alkali) passes through a cavity in which different lasers send pulses to the atoms. These pulses alter the state of the electron and bring it to the desired state. In our case, the superposition of circular states. The main problem is that the pulses that are needed are not easy to find.

It is then when the theoretical physicists provide some help with a powerful tool: optimal control. They use some algorithms (such as Krotov’s algorithm) to find out a good laser pulse that could achieve the main objective. But the problem is not so simple. Sometimes these pulses are quite messy, and cannot be exactly reproduced at the lab. Both theoreticians and experimentalists have to cooperate to refine the solution, so it can finally be implemented in the real experiment. Once a feasible solution is found, it can be used as many times as we want to prepare all our atoms.
And there we have it, a full set of quantum compasses fresh out of the oven!


