08 Jan How does a quantum computer work?
Max Werninghaus
Quantum physics: the building blocks of our universe
More than a hundred years ago, in the time of brilliant scientists such as Albert Einstein, researchers were trying to make sense of the very smallest objects of our universe. More and more discoveries led to the theory of quantum physics, which was able to describe the structure of individual atoms and the behavior of light particles, the so-called quantum particles. Very soon after the world of quantum mechanics was discovered, a famous scientist named Richard Feynman proposed to build a computing machine which could tap into the potential power of this complicated and abstract world. The main motivation was the simple fact that nature is fundamentally built and defined by the laws of quantum mechanics. The logical conclusion is that in order to calculate and predict the behavior of nature we should build a computer which follows the same principles.
Nowadays we know that difficult problems of everyday situations could be solved extremely quickly by a quantum computer with enough computational power.
How do these computers work?
Just like a processor in a laptop or smartphone, a quantum computer solves problems by performing operations on bits. Bits are very simple building blocks which can either display a zero, or a one. By combining millions of bits, a computer can work with large numbers very well. By changing the states of these bits, a computer can rapidly perform mathematical operations such as addition and multiplication. A quantum bit, also called qubit, behaves in principle in the same way as a normal, or classical Bit, however it can be in both zero and one at the same time; we call this special state a superposition state. This superposition state is possible because of the laws of quantum physics and it gives quantum computers such an immense computational power, that the entire information on the internet could be displayed by just 64 quantum bits – this corresponds to a memory amount of 134 million gigabytes.
Calculations on a quantum computer are performed by altering the state of the quantum bits in a similar way as on a normal computer. However, since we can be in zero and one simultaneously, we can perform calculations of all possible numbers at the same time. As powerful as it is, mastering quantum computation is difficult and must be performed with great precision.
Controlling quantum operations
Imagine a qubit operation as trying to hit a target from far away, as shown in the illustration below.

To make it even more difficult, if we do not hit it precisely, we have to step a certain distance away from the target, depending on how far we missed it. That means if we are slightly off target, each following shot will be less and less likely to hit the target correctly. This corresponds to the qubit changing its internal state exactly as we intend it to, such that our computation will function correctly. To perform correct calculations, we need to hit our target as precisely as possible every time, otherwise mistakes will compound and the final result will be wrong. With our first try, we will probably not be able to score perfectly, but we can learn why we missed and try to improve with the next one by calibrating our shot.
In the same way, we try to improve the way we steer the quantum operations acting on the quantum bits. We provide the quantum bit with an energy pulse, that is used to perform a quantum operation, the quantum counterpart to the operations of normal Bits. Many of those operations are needed to find the solution for difficult problems. The success of these operations is a direct result of how we provide the energy. By carefully tweaking the energy pulse we give to the quantum bit, we can improve our precision and hit the target state almost perfectly. The more time we spend on improving the pulses the more we can learn about the reason why we missed. This allows us to improve our operations so that next time, hitting the target is almost assured.
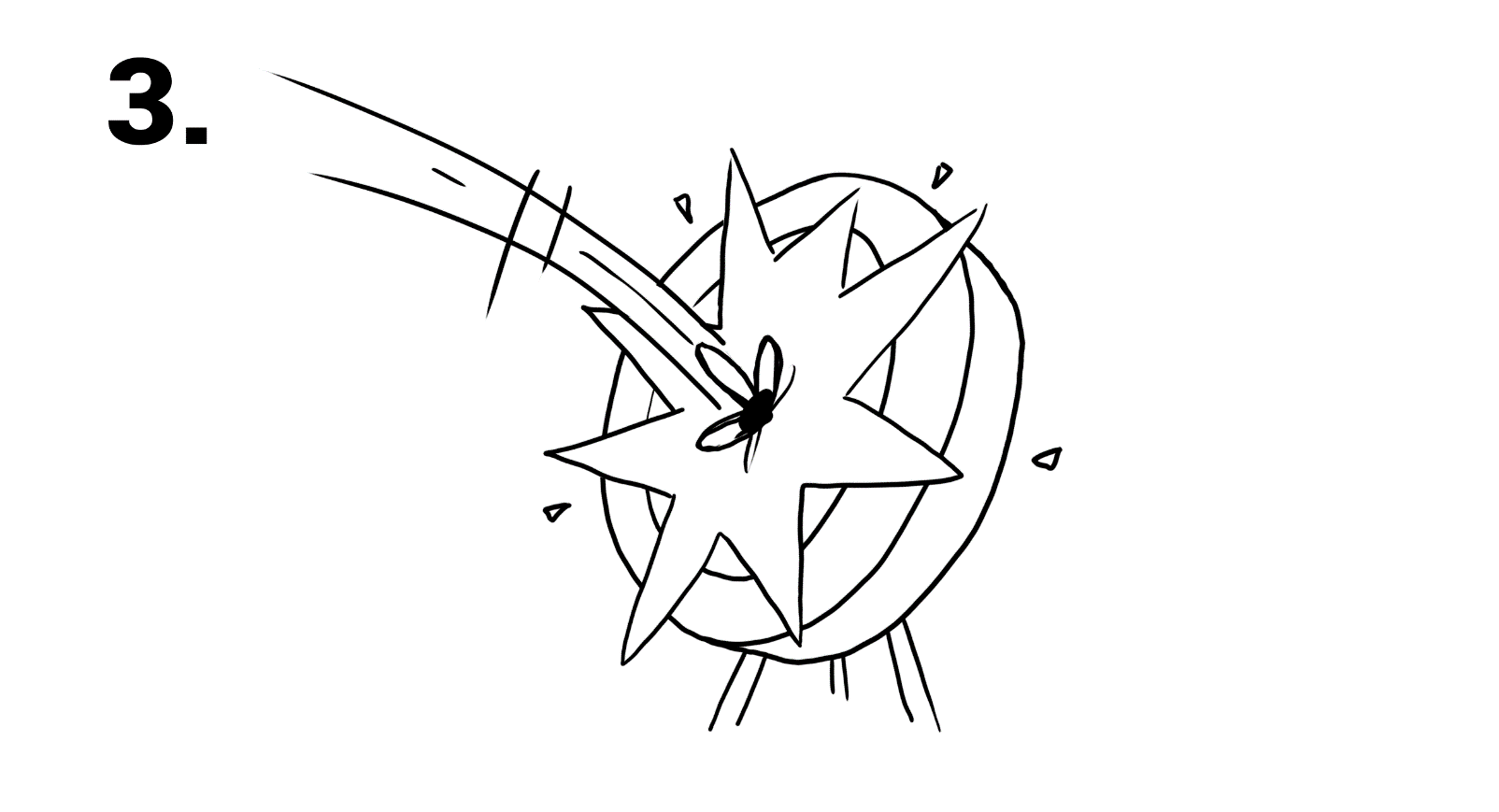
Only if we provide a precise enough energy pulses to the quantum bits can we be sure that our quantum calculations will be correct. In my research I am working to understand how these energy pulses interact with the qubits and try to improve the control of quantum operations.
How do we build computers from this?
In the current state of quantum computers, we are building quantum bits out of individual, small quantum systems, so its performance directly depends on the performance of our quantum operations. Machines like these can already be used to learn about other quantum systems like simple molecules and chemical reactions; In order to use quantum computers for actual numerical computations, we also need some fault tolerant methods in place. We have concepts which use multiple quantum particles to correct each other such that mistakes are more easily corrected. One simple example is the concept of a majority vote: Here, for example three quantum bits together decide on the state they represent. They should all be the same if no mistakes happened, but if one of them is in a wrong state the other two will overrule it and correct the error. Modern computers have similar techniques in place. To achieve this in a quantum device however, we need to reach a certain threshold of accuracy in our operations. There is still a long research period ahead of us, but once we have mastered the full power of a quantum computer, we will be able to use the complexity of quantum physics to perform immense calculations and understand natures fundamental building blocks to a never known precision.


