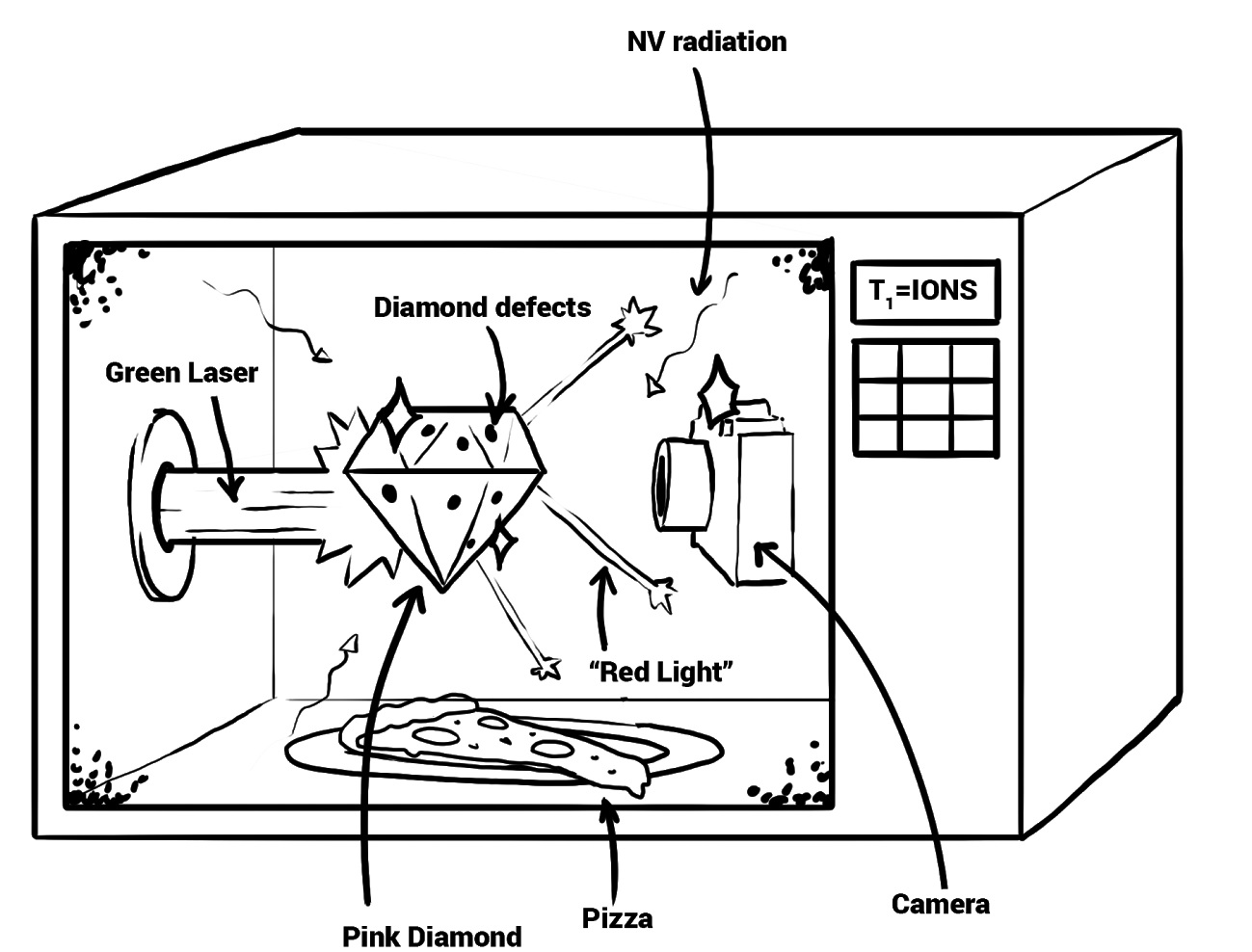
30 Sep How to Microwave a Diamond
Diamonds, as Shirley Bassey once sang, are “forever, forever, forever” in part because diamonds are an incredibly tough material. Mined from deep pits in the Earth before being polished and cut to glister on expensive jewellery, they are the ultimate status symbol. But diamonds aren’t just for showing off, their chemical stability makes them ideal for a range of applications all across science. Natural diamonds are formed when deposits of Carbon are compressed at high temperature deep underground. The huge amount of effort expended to extract them is what makes them so valuable and you can’t guarantee their purity. So you might wonder how physicists like me are able to get our hands on them. The answer is simple; we grow them. Synthetic diamonds are produced in labs around the world and are available for a fraction of the price of a similar quality natural sample. There are two main growing techniques, which I won’t go into here, called chemical vapour deposition (CVD) and high pressure, high temperature (HPHT) growth.
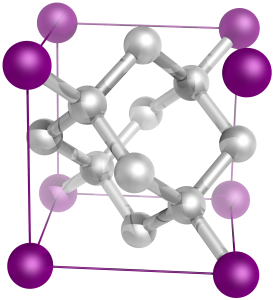
By closely monitoring and adjusting the environment in which these diamonds are grown, it becomes possible to introduce defects into their structure. Diamond normally forms a lattice structure, shown in the figure below, but it is possible to disturb this periodic structure to create a point defect. The defect that I focus on in my work are those created by a substitutional nitrogen atom replacing a carbon and leaving a neighbouring lattice site vacant. This is the so called nitrogen vacancy centre or NV centre. Some of the diamonds that I use are actually a dark purple colour (almost black) because they have so many of these defects.
Well, you may ask, purple diamonds are all well and good, but what can we do with them? One special property of the NV centre is that it can be optically initialised and readout. The centre is a spin 1 system which means it has 3 magnetic sublevels, -1, 0 and +1. Light emitted by the centre is state dependent, the +1 and -1 states are more likely to cross over to a so-called dark state and emit fewer photons. If we can precisely measure this difference in photons then we can determine what state our system is in.

Without a magnetic field present, the -1 and +1 levels are energy degenerate, this simply means that they have the same energy and so we cannot tell them apart! If you bring a magnet near the diamond the NV centre, energy levels undergo Zeeman splitting, which causes them to no longer have the same energy. But we must add one final component before we have complete control over our quantum state in this microscopic quantum computer: microwaves.
Unfortunately we’re not talking about your common everyday microwave at home, but instead a small microwave antennae sitting on the surface of the diamond. Most often, we just use a small piece of copper wire connected to a specially designed sample holder. With the levels split (because of the magnet that we brought close to the diamond), we can treat the -1, 0 levels as a two level system and just ignore the 1 state. This is the basis of a solid-state qubit, which we are able to manipulate by applying the correct pulse sequence.
So we have taken a diamond with some particular defects (nitrogen vacancies) and applied a magnetic field in order to split apart the energy levels. We have then exploited the state dependent emission rate so that we can accurately determine the state of the system and, using microwaves, manipulate it. This all happens at an atomic scale within a few hundred microseconds and all at room temperature in an optics lab.
This begins to hint at the true power of the NV centre as a miniature quantum sensor for small fields. In order to achieve good sensitivity we design specific microwave sequences, which are, hopefully, sensitive to frequencies of interest and limit as much as possible the amount of noise we collect. Over the years many such sequences have been devised which are analytically designed to work well in specific situations. However when we want to push our sequences even further we turn to quantum optimal control.
Quantum optimal control describes a set of tools for a quantum engineer to use in order to enhance the control of their system. This field has seen a lot of attention in recent years as people start to demand sequences that can perform well in a variety of tough experimental situations. Using numerical algorithms, we can begin to shape the microwave pulse sequences, the ones that we use to manipulate the quantum state, to take into account experimental constraints or improve sequence stability. The limiting factor is no longer, whether you can analytically find an optimal sequence, but instead how large a system and how many factors can you include in the numerical optimisation. These numerical techniques can be very powerful.
So by microwaving a diamond we can manipulate a tiny quantum system and begin to dream up interesting things to do with it. Using numerical algorithms to structure the microwaves that we apply allows us to push these limits even further.


